При математической обработке количественных показателей, сведенных в аналитические таблицы (вариационный ряд), обычно ограничиваются вычислением средней арифметической (М) и ее ошибки (m). Величину средней арифметической определяют путем деления сумм показателей вариационного ряда (вариантов — Y) на количество вариант (n) по формуле:

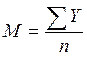
Ошибку средней арифметической (m) можно сравнительно легко вычислить константным методом по формуле:

, где

К — константа, отыскиваемая по таблице А в ряду равной количеству вариантов, участвующих в выборке (n);

— сумма величин отклонений вариант (больше или меньше) от величины средней арифметической (Y-M).

Таблица А

Число вариантов, а	Величина константы
5	0,1253
6	0,0934
7	0,0731
8	0,0592
9	0,0492
10	0,0418
11	0,0360
12	0,0315
13	0,0278
14	0,0248
15	0,0223

ПРИМЕР: определите величину средней арифметической (М) и величину ее ошибки (m) показателей уровня вакцинации по таблице 10.

Таблица Б

Ряд 1	Варианты (Y)	55,1	57,3	63,2	64,7	62,6	68,6	70,9	75,2	74,0	77,5
Ряд 2	Отклонения от М (а)	11,8	9,6	3,7	2,2	4,3	1,7	4,0	8,3	7,1	10,6

В этом ряду 10 показателей (вариантов Y) — это показатели уровня вакцинации за 1991 — 2000 гг., n=10

1.  Определяют величину средней арифметической ряда.

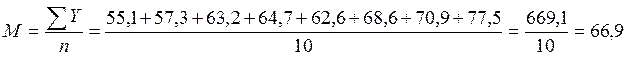
Средняя арифметическая равна 66,9.

2.  Определяют отклонение каждой варианты (показателя уровня вакцинации за каждый год) от величины средней арифметической. Для этого показатели вакцинации за 1991-2000 гг. располагают в таблицу Б, ряд 1 и определяют величину отклонения (а), ряд 2 (Y-M). Затем их суммируют без учета арифметических знаков, полученную сумму умножают на константу (таблица А) по строке числа вариантов 10, который в данном случае равен 0,0418, получают величину ошибки средней арифметической.

Итак, в нашем примере

1.  количество вариантов n=10;

2.  средняя арифметическая М=66,9;

3.  Константа (при n=10) – К = 0,0418;

4.  Сумма отклонений вариантов от средней арифметической ∑а=63,3. Ошибка средней арифметической m=K×∑а=0,0418×63,3=2,6459; 2,65

М±m=66,9±2,65