МЕТОДИКА ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА РАНГОВОЙ КОРРЕЛЯЦИИ
Коэффициент ранговой корреляции позволяет измерить тесноту связи между двумя взаимодействующими явлениями (например: влияние уровня вакцинации на заболеваемость животных, увеличение популяции грызунов / лисиц на распространение лептоспироза / бешенства). Его величина может колебаться в пределах от —1 до +1. В пределах от 0 до +1 указывает на прямую (положительную) корреляционную связь между явлениями, то есть такую связь, когда увеличение одного признака (явления) соответствует увеличению другого признака. Изменение в пределах от 0 до —1 значения коэффициента ранговой корреляции указывает на тесноту обратной (отрицательной) связи между явлениями, т. е. когда увеличение одного признака соответствует уменьшению другого.
Считают, что величина коэффициента ранговой корреляции до 0,50 отражает слабую связь между явлениями, от 0,50 до 0,80 среднюю, а более 0,80 сильную степень связи. Пример: определить коэффициент ранговой корреляционной связи между уровнем вакцинации и заболеваемостью по данным табл..
Для этого:
1. Показатели уровня вакцинации обозначают буквой X, а показатели заболеваемости буквой Y и вписывают их в таблицу В.
2. Каждому показателю вакцинации и заболеваемости за
определенный год присваивают порядковый номер в зависимости от абсолютной величины показателя. При этом порядковый номер 1 присваивают самому большому показателю и т. д., самый малый показатель получает самый большой порядковый (номер, который вписывают в соответствующие строки таблицы В, графу 4 (номера показателей вакцинации) и графу 5 (номера показателей заболеваемости). Если несколько показателей имеют одинаковую величину, то им одинаковый порядковый номер присваивать нельзя, а дают последующий порядковый номер по усмотрению исследователя.
3. Определяют разность (Д) между величинами порядкового номера показателя вакцинации (X) и заболеваемости (Y) по каждой строке и вписывают их в графу 6.
4. Показатели разностей порядковых номеров по каждой строке возводят в квадрат (Д2) и вписывают в графу 7 табл. В.
5. Находят сумму квадратов разностей порядковых номеров (по графе 7) путем их сложения /∑Д2/.
6. коэффициент ранговой корреляции (r-ранг) определяют по формуле
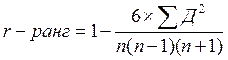
Таблица В
|
Годы |
Вакцинировано %, Х |
Заболеваемость Y |
Порядковые номера |
Д |
Д2 |
|
|
Х |
Y |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1991 |
55,1 |
0.28 |
10 |
2 |
8 |
64 |
|
1992 |
57,3 |
0,17 |
9 |
3 |
6 |
36 |
|
1993 |
63,2 |
0,21 |
7 |
1 |
6 |
36 |
|
1994 |
64,7 |
0.16 |
6 |
4 |
2 |
4 |
|
1995 |
62,6 |
0,12 |
8 |
6 |
2 |
4 |
|
1996 |
68,6 |
0,14 |
5 |
5 |
0 |
0 |
|
1997 |
70,9 |
0,09 |
4 |
7 |
3 |
9 |
|
1998 |
75,2 |
0,08 |
2 |
8 |
6 |
36 |
|
1999 |
74,0 |
0,08 |
3 |
9 |
6 |
36 |
|
2000 |
77,5 |
0,06 |
1 |
10 |
9 |
81 |
|
Сумма Д2 =306 |
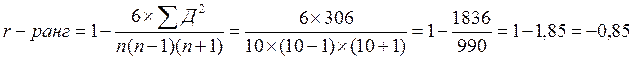
В нашем примере коэффициент ранговой корреляции равен – 0,85. Это значит, что между уровнем вакцинации животных и заболеваемостью наблюдается обратная корреляционная зависимость сильной степени, т. е. с увеличением количества вакцинированных животных происходит значительное снижение заболеваемости.

