Количественные закономерности действия лекарств. Закон уменьшения отклика биологических систем. Модель Кларка и ее следствия. Общий вид зависимости концентрация – эффект в нормальных и логнормальных координатах.
Модель Кларка-Ариенса:
1. Взаимодействие между лигандом (L) и рецептором (R) обратимы.
2. Все рецепторы для данного лиганда – эквивалентны и независимы (их насыщение не влияет на другие рецепторы).
3. Эффект прямо пропорционален числу занятых рецепторов.
4. Лиганд существует в двух состояниях: свободном и связанном с рецептором.
А) ![]() , где Kd – константа равновесия, Ke – внутренняя активность.
, где Kd – константа равновесия, Ke – внутренняя активность.
Б) Т. к. при возрастании количества лигандов в какой-то момент времени все рецепторы окажутся заняты, то максимально возможное количество образованных комплексов лиганд-рецептор описывается формулой:
Эффект определяется вероятностью активации рецептора при связывании с лигандом, т. е. его внутренней активностью (Ке), поэтому E = Ke×[RL]. При этом эффект максимален при Ке=1 и минимален и Ке=0. Естественно, что максимальный эффект описывается соотношением Emax = Ke×[Rобщий], где [Rобщий] – общее число рецепторов для данного лиганда
Эффект зависит и от концентрации лиганда на рецепторах [С], поэтому
E = Emax 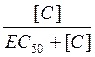 (2)
(2)
Из приведенных соотношений вытекает, что EC50=Kd
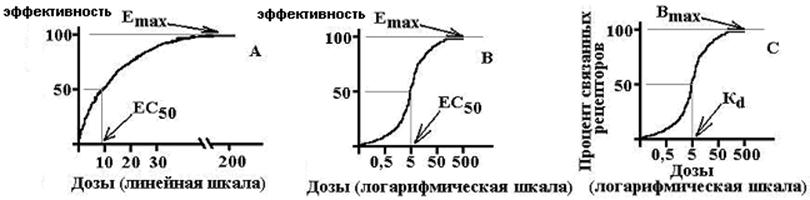
Emax – максимальный эффект, Bmax – максимальное число связанных рецепторов, EC50 – концентрация ЛС, при которой возникает эффект, равный половине от максимального, Kd – константа диссоциации вещества от рецептора, при которой связано 50% рецепторов.
Закону убывания отклика соответствует параболическая зависимость «концентрация – эффективность». Ответ на малые дозы ЛС обычно возрастает прямо пропорционально дозе. Однако при увеличении дозы прирост ответной реакции снижается и в конечном счете может быть достигнута доза, при которой не происходит дальнейшего увеличения ответа (за счет оккупации всех рецепторов для данного лиганда).


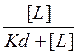 (1)
(1)